 Prawo idealnego odbicia mówi, iż kąt odbicia (angle of reflection) równa się kątowi padania (angle of incidence). Stąd, w idealnym prostokątnym bilardzie, by kulą A uderzyć kulę B poprzez jedno odbicie o bandę stołu bilardowego, należy mierzyć w wyobrażone odbicie lustrzane kuli B w bandzie. Ponieważ prostokąt ma cztery boki, cztery możliwe odbicia staną się rozwiązaniem problemu.
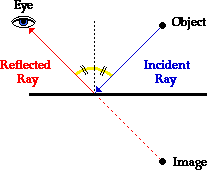
Prawo idealnego odbicia mówi, iż kąt odbicia (angle of reflection) równa się kątowi padania (angle of incidence). Stąd, w idealnym prostokątnym bilardzie, by kulą A uderzyć kulę B poprzez jedno odbicie o bandę stołu bilardowego, należy mierzyć w wyobrażone odbicie lustrzane kuli B w bandzie. Ponieważ prostokąt ma cztery boki, cztery możliwe odbicia staną się rozwiązaniem problemu.
Pod poprzednią notką, komentator ‘teddi22’ zapytał o przepis na podobne odbicie w bilardzie kołowym. Oto kule A i B spoczywają wewnątrz okręgu, i kulę A należy odbić w okręgu tak, by po odbiciu uderzyła w kulę B. To samo prawo odbicia wciąż rządzi – nie tylko zresztą dla okręgu, lecz dla dowolnej krzywej gładkiej. Przez „gładkość” rozumiemy istnienie linii stycznej w każdym punkcie, a więc również prostopadłej do niej – tzw. linii normalnej. Zatem owe prawo równości kątów odbicia i padania zachodzi względem prostej normalnej do krzywej w punkcie odbicia.
Tu – dygresja: dlaczego prosta prostopadła nazywa się „normalną” (podobnie – dlaczego wektor prostopadły do krzywej czy powierzchni zwie się „wektorem normalnym”). Słowo „norma” po łacinie było nazwą węgielnicy, przyrządu służącego do wskazywania kąta prostego. Zatem – „normalny” oznacza „prosty” lub „prostopadły”. Na nocnym południowym niebie widnieje nawet gwiazdozbiór o nazwie Węgielnica lub Norma, ukazany na obrazku z lewej. Klik na obrazek prowadzi do strony, gdzie wiecej o „normie” można poczytać, między innymi o etymologii słowa...
Wracając do naszych kul... Teddiego interesowało jeszcze odbijanie z „podkręceniem” – jak i gdzie odbić, gdy kula obraca się, przez co powyższe prawo równości kątów odbicia i padania przestaje obowiązywać (zastąpione przez nowe prawo). Jednak, nawet bez obrotu zadanie nie nie jest łatwe. Można je uprościć, rozważając „bile” punktowe – wystarczy śledzić ruch środków danych kul, zmniejszając okrąg bilardu o ich promień. Moim pierwszym wrażeniem było przekonanie, iż jest to jeden z problemów antycznych, albowiem pytanie wydaje się być raczej naturalne, i takoż w antyczności musiało być – tak myślałem – już rozwiązane.
Własna próba rozwiązania, np. oparta na twierdzeniu kosinusów, prowadziła do wielce powikłanego równania czwartego stopnia. Inne podejścia, czy przy użyciu algebry liniowej i macierzy obrotów, czy przy pomocy liczb zespolonych, również kończyły się nieprzyjemnymi równaniami trygonometrycznymi, bądź, po redukcji –znów równaniami stopnia czwartego.
Odbijać jest łatwo, ale trafić w cel – już nie. Łatwo napisać jest równanie, gorzej – rozwiązać. Na przykład, spróbujmy użyć liczb zespolonych. Rozważmy okrąg jednostkowy, czyli zbiór punktów postaci exp{it}, gdzie t przebiega odcinek [0,2π), i „t” może być intepretowane dynamicznie - jako kąt zakreślony przez punkt poruszajacy się po okręgu jednostkowym ze stałą jednostkową prędkością kątową. Punkt zaczyna swą podróż od pozycji (1,0) we współrzędnych kartezjańskich, i porusza się wkierunku dodatnim, przeciwnym do kierunku ruchu wskazówek typowego zegara. „Typowego” –albowiem istnieją wszak wyjątkowe zegary, których wskazówki biegną na odwrót...
Nasze bile – to dane liczby zespolone u i v, |u|<1, |v|<1. Wykorzystując prawo Fermata – iż promień świetlny porusza się po najkrótszej trajektorii – zadanie sprowadza się do znalezienia minimum funkcji
![\left|e^{it}-u|+\left|e^{it}-v\right| [; \left|e^{it}-u|+\left|e^{it}-v\right| ;]](http://www.codecogs.com/gif.latex? \left|e^{it}-u|+\left|e^{it}-v\right|)
Tak – łatwo napisać, trudno rozwiązać.
Niemniej, znaleźli się dzielni, którzy nie przestraszyli się równania stopnia czwartego. Wzięli się, zawzięli... i rozwiązali. Nie byli to antyczni Grecy, albowiem rzecz została wyjaśniona raptem w latach 90-tych ubiegłego stulecia. Wśród kilku rozwiązań najbardziej eleganckie wydaje mi się następujące:
Michael Drexler & Martin J. Gander: Circular Billiard, SIAM Rev., 1998 40(2), 315–323
(pdf do pobrania w prawym górnym rogu)
Posiada ono przyjemną intepretację geometryczną, opierającą się na wspomnianym prawie Fermata, choć pośrednio. Mianowicie, promień świetlny wychodzący z ogniska elipsy, i odbity w niej, trafia do drugiego ogniska. Owe odbicia wewnątrz elipsy fascynowały mnie już kilka lat temu, i pewnym im aspektom poświęciłem notkę ”Włochate Eli Psy”.
Zatem, by znaleźć punkt odbicia, by trajektoria z punktu A po odbiciu przeszła przez punkt B, należy te punkty uczynić ogniskami elipsy stycznej do danego okręgu. Odcinek AB jest zdegenerowaną, sflaczałą elipsą o maksymalnym mimośrodzie (eccentricity) równym 1, jego końce są zarazem ogniskami. Należy ją zatem nadmuchać poprzez zmniejszanie mimośrodu tak, by nadmuchana elipsa zetknęła się z okręgiem. Jak widać z ilustracji, zapożyczonej z pracy Drexlera i Gandera, mogą być dwa, a mogą być nawet cztery rozwiązania.

Metoda nadmuchiwania elipsy aż do jej zetknięcia z krzywą stosuje się do dowolnej krzywej gładkiej, byle by ona nie przecinała odcinka łączącego punkty A i B.

